光海被对手包围那一刻的有趣几何问题
借鉴越南选手在半决赛第二回合对阵菲律宾队的比赛中的精彩瞬间,尝试解答以下几何问题。
12月6日,在河内美亭体育场举行的2018年东南亚足球锦标赛半决赛第二回合比赛中,阮光海被评为最佳球员。以下题目灵感源自阮光海在菲律宾球员围攻中奋力拼搏的瞬间。。
|
图像:林托 |
话题:
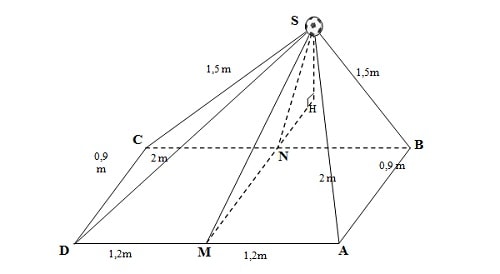
上图显示,四名菲律宾球员正围着顾光海持球。假设SABCD是一个金字塔,球位于金字塔顶端S,底面ABCD是一个包含五名球员的平行四边形,其中A、B、C、D四个顶点分别代表最左和最右两名菲律宾球员的脚。设M和N分别为顾光海的右脚落地点和面对顾光海的菲律宾球员的右脚落地点。
已知AD=BC=2.4米;AB=CD=0.9米;SA=SD=2.0米;SB=SC=1.5米;M、N分别为AD、BC的中点。
1. 计算 (SM; SN) 形成的角度。
2. 计算球到平面的距离(ABCD).
问题:
上图显示,Quang Hai 被四名菲律宾足球运动员包围,四人均持球。假设 SABCD 是一个金字塔,顶点 S 是球,底面 ABCD 是一个包含所有五名足球运动员的平行四边形,顶点 A、B、C 和 D 分别代表左右两名菲律宾球员的脚部位置。令 M 和 N 分别代表 Quang Hai 的右脚位置和他右脚的对侧脚位置。
已知 AD = BC = 2.4 m;AB = CD = 0.9 m;SA = SD = 2.0 m;SB = SC = 1.5m;M 和 N 分别是 AD 和 BC 的中点。
1. 计算角度的度数(SM;SN)。
2.计算球与表面(ABCD)之间的距离。
|