Interesting geometry problem from the moment Quang Hai was surrounded by opponents
From the impressive moment of the Vietnamese player in the second leg of the semi-final against the Philippines, try solving the following geometry problem.
In the second leg of the AFF Cup 2018 semi-final on December 6 at My Dinh Stadium, Hanoi, Quang Hai was voted the best player. The following problem was inspired by the moment Quang Hai fought fiercely in the siege of Filipino players..
|
Image:Lam Thoa |
Topic:
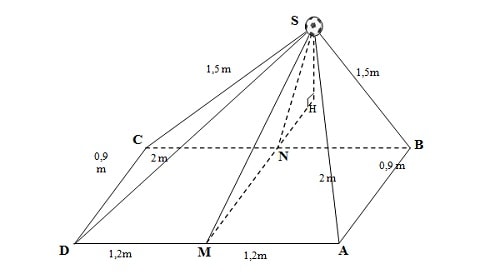
The picture above shows Quang Hai surrounded by 4 Filipino players with the ball. Suppose SABCD is a pyramid with the ball at the top S and the base ABCD is a parallelogram containing all 5 players, in which the 4 tops A, B, C, D are the feet of the 2 Filipino players on the far left and right. Let M and N be the landing points of Quang Hai's right foot and the right foot of the Filipino player facing Quang Hai, respectively.
Knowing AD = BC = 2.4 m; AB = CD = 0.9 m; SA = SD = 2.0 m; SB = SC = 1.5 m; and M and N are the midpoints of AD and BC.
1. Calculate the angle formed by (SM; SN).
2. Calculate the distance from the ball to the plane (ABCD).
Problem:
The image above shows Quang Hai surrounded by 4 Filipino footballers with the ball. Assume that SABCD is a pyramid where apex S is the ball and base ABCD is a parallelogram containing all 5 footballers, in which vertices A, B, C, and D represent the foot positions of 2 Filipinos on the left and the right. Let M and N be the right foot position of Quang Hai and his immediate opposite respectively.
Given that AD = BC = 2.4 m; AB = CD = 0.9 m; SA = SD = 2.0 m; SB = SC = 1.5m; and M and N are the midpoints of AD and BC.
1. Calculate the measure of angle (SM; SN).
2.Calculate the distance between the ball and surface (ABCD).
|