Интересная задача по геометрии с того момента, как Куанг Хай был окружен противниками.

В ответном матче полуфинала Кубка АФФ-2018, состоявшемся 6 декабря на стадионе «Ми Динь» в Ханое, Куанг Хай был признан лучшим игроком. Следующая задача была вдохновлена ​​моментом, когда Куанг Хай яростно сражался с филиппинскими игроками, осаждавшими его..

Тема:

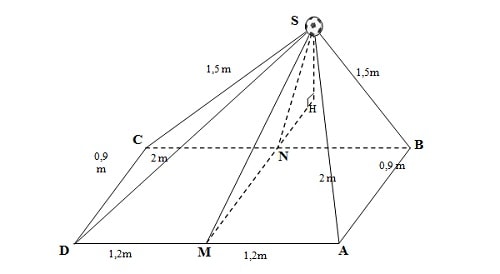
На рисунке выше изображён Куанг Хай в окружении четырёх филиппинских игроков с мячом. Предположим, что SABCD — пирамида с мячом на вершине S, а основание ABCD — параллелограмм, содержащий всех пяти игроков. Четыре вершины A, B, C и D — это ступни двух филиппинских игроков слева и справа. Пусть M и N — точки приземления правой ноги Куанг Хай и правой ноги филиппинского игрока, стоящего напротив Куанг Хай, соответственно.

Зная, что AD = BC = 2,4 м; AB = CD = 0,9 м; SA = SD = 2,0 м; SB = SC = 1,5 м; а M и N — середины AD и BC.

1. Рассчитайте угол, образованный (SM; SN).

2. Рассчитайте расстояние от мяча до плоскости (ABCГ).

Проблема:

На изображении выше изображён Куанг Хай в окружении четырёх филиппинских футболистов с мячом. Предположим, что SABCD — пирамида, вершина S которой — мяч, а основание ABCD — параллелограмм, содержащий всех пяти футболистов. Вершины A, B, C и D соответствуют положению ног двух филиппинцев слева и справа. Пусть M и N — положение правой ноги Куанг Хая и его прямой противоположной ноги соответственно.

Учитывая, что AD = BC = 2,4 м; AB = CD = 0,9 м; SA = SD = 2,0 м; SB = SC = 1,5 м; а M и N являются серединами AD и BC.

1. Вычислите величину угла (SM; SN).

2.Рассчитайте расстояние между мячом и поверхностью (ABCD).