Problème de géométrie intéressant à partir du moment où Quang Hai était encerclé par des adversaires

Lors du match retour de la demi-finale de la Coupe AFF 2018, le 6 décembre au stade My Dinh de Hanoï, Quang Hai a été élu meilleur joueur. Le problème suivant s'inspire de son combat acharné contre des joueurs philippins..

Sujet:

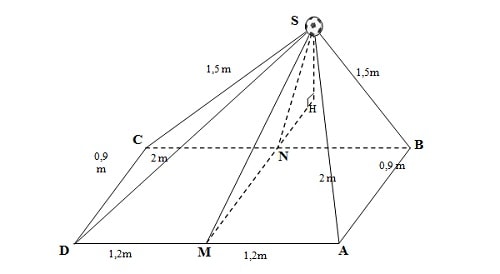
L'image ci-dessus montre Quang Hai entouré de quatre joueurs philippins avec le ballon. Supposons que SABCD soit une pyramide dont le sommet est S et la base ABCD un parallélogramme contenant les cinq joueurs. Les quatre sommets A, B, C et D sont les pieds des deux joueurs philippins les plus à gauche et à droite. Soient M et N les points d'atterrissage du pied droit de Quang Hai et du pied droit du joueur philippin faisant face à Quang Hai, respectivement.

Sachant que AD = BC = 2,4 m ; AB = CD = 0,9 m ; SA = SD = 2,0 m ; SB = SC = 1,5 m ; et que M et N sont les points médians de AD et BC.

1. Calculez l'angle formé par (SM; SN).

2. Calculez la distance entre la balle et le plan (ABCD).

Problème:

L'image ci-dessus montre Quang Hai entouré de quatre footballeurs philippins avec le ballon. Supposons que SABCD soit une pyramide dont le sommet S est le ballon et la base ABCD un parallélogramme contenant les cinq footballeurs, dont les sommets A, B, C et D représentent les positions des pieds de deux Philippins à gauche et à droite. Soient M et N les positions des pieds droit de Quang Hai et de son opposé immédiat, respectivement.

Étant donné que AD = BC = 2,4 m ; AB = CD = 0,9 m ; SA = SD = 2,0 m ; SB = SC = 1,5 m ; et M et N sont les points médians de AD et BC.

1. Calculez la mesure de l'angle (SM ; SN).

2.Calculez la distance entre la balle et la surface (ABCD).